神经网络

神经网络-算法

类似于神经元的神经网络，效果如下：

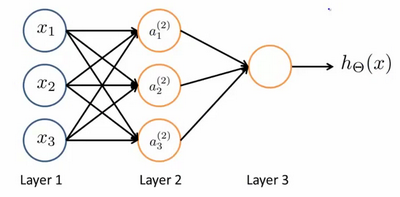
其中 $x_{1}$ , $x_{2}$ , $x_{3}$ 是输入单元（input units），我们将原始数据输入给它们。 $a_{1}$ , $a_{2}$ , $a_{3}$ 是中间单元，它们负责将数据进行处理，然后呈递到下一层。

最后是输出单元，它负责计算 $h_{\theta}(x)$ 。

神经网络模型是许多逻辑单元按照不同层级组织起来的网络，每一层的输出变量都是下一层的输入变量。下图为一个3层的神经网络，第一层成为输入层（Input Layer），最后一层称为输出层（Output Layer），中间一层成为隐藏层（Hidden Layers）。我们为每一层都增加一个偏差单位（bias unit）：

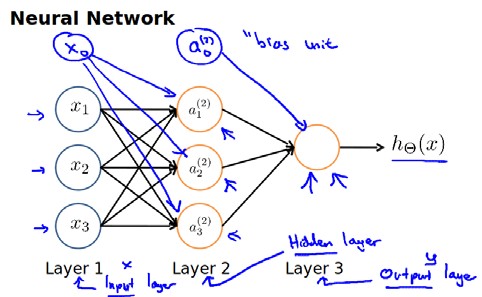
下面引入一些标记法来帮助描述模型：

$a_{i}^{(j)}$ 代表第 $j$ 层的第 $i$ 个激活单元。 $\theta^{(j)}$ 代表从第 $j$ 层映射到第 $j+1$ 层时的权重的矩阵，例如 $\theta^{(1)}$ 代表从第一层映射到第二层的权重的矩阵。其尺寸为：以第 $j+1$ 层的激活单元数量为行数，以第 $j$ 层的激活单元数加一为列数的矩阵。例如：上图所示的神经网络中的 $\theta^{(1)}$ 尺寸为 3*4。

对于上图所示的模型，激活单元和输出分别表达为：

$a_{1}^{(2)}=g\left(\theta_{10}^{(1)} x_{0}+\theta_{11}^{(1)} x_{1}+\theta_{12}^{(1)} x_{2}+\theta_{13}^{(1)} x_{3}\right)$

$a_{2}^{(2)}=g\left(\theta_{20}^{(1)} x_{0}+\theta_{21}^{(1)} x_{1}+\theta_{22}^{(1)} x_{2}+\theta_{23}^{(1)} x_{3}\right)$

$a_{3}^{(2)}=g\left(\theta_{30}^{(1)} x_{0}+\theta_{31}^{(1)} x_{1}+\theta_{32}^{(1)} x_{2}+\theta_{33}^{(1)} x_{3}\right)$

$h_{\theta}(x)=g\left(\theta_{10}^{(2)} a_{0}^{(2)}+\theta_{11}^{(2)} a_{1}^{(2)}+\theta_{12}^{(2)} a_{2}^{(2)}+\theta_{13}^{(2)} a_{3}^{(2)}\right)$

每一个 $a$ 都是由上一层所有的 $x$ 和每一个 $x$ 所对应的决定的。（我们把这样从左到右的算法称为前向传播算法( FORWARD PROPAGATION )）

把 $x$ , $\theta$ , $a$ 分别用矩阵表示，我们可以得到 $\theta \cdot X=a$ ：

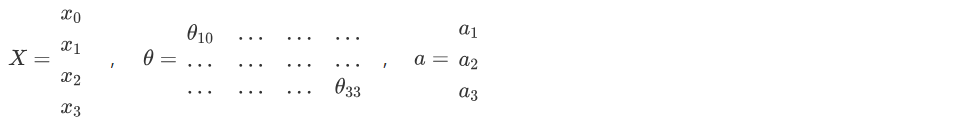
相对于使用循环来编码，利用向量化的方法会使得计算更为简便。以上面的神经网络为例，试着计算第二层的值：

$z^{(2)}=\theta^{(1)} x$

$a^{(2)}=g\left(z^{(2)}\right)$

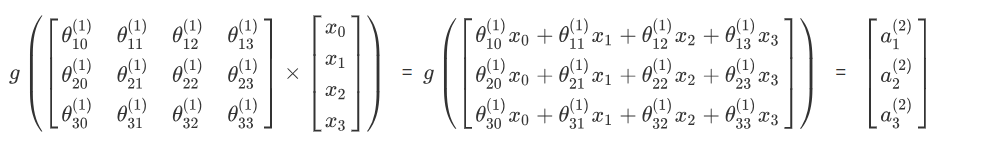
我们令 $z^{(2)}=\theta^{(1)} x$ ，则 $a^{(2)}=g\left(z^{(2)}\right)$ ，计算后添加 $a_{0}^{(2)}=1$ 。 计算输出的值为：

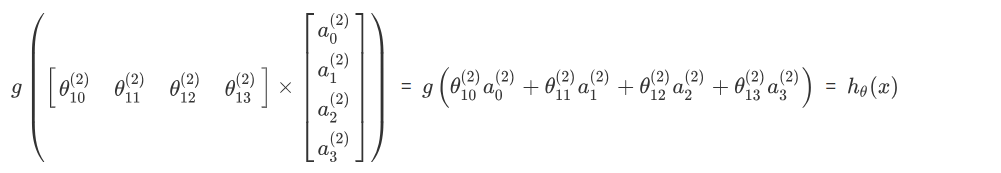
我们令 $z^{(3)}=\theta^{(2)} a^{(2)}$ ，则 $h_{\theta}(x)=a^{(3)}=g\left(z^{(3)}\right)$

这只是针对训练集中一个训练实例所进行的计算。如果我们要对整个训练集进行计算，我们需要将训练集特征矩阵进行转置，使得同一个实例的特征都在同一列里。即：

$z^{(2)}=\theta^{(1)} \times X^{T}$

$a^{(2)}=g\left(z^{(2)}\right)$

其实神经网络就像是logistic regression，只不过我们把logistic regression中的输入向量 $\left[x_{1} \sim x_{3}\right]$ 变成了中间层的 $\left[a_{1}^{(2)} \sim a_{3}^{(2)}\right]$ , 即:

$h_{\theta}(x)=g\left(\theta_{0}^{(2)} a_{0}^{(2)}+\theta_{1}^{(2)} a_{1}^{(2)}+\theta_{2}^{(2)} a_{2}^{(2)}+\theta_{3}^{(2)} a_{3}^{(2)}\right)$

我们可以把 $a_{0}$ , $a_{1}$ , $a_{2}$ , $a_{3}$ 看成更为高级的特征值，也就是 $x_{0}$ , $x_{1}$ , $x_{2}$ ,$x_{3}$ 的进化体，并且它们是由 $x$ 与决定的，因为是梯度下降的，所以 $a$ 是变化的，并且变得越来越厉害，所以这些更高级的特征值远比仅仅将 $x$ 次方厉害，也能更好的预测新数据

反向传播算法

之前我们在计算神经网络预测结果的时候我们采用了一种正向传播方法，我们从第一层开始正向一层一层进行计算，直到最后一层的 $h_{\theta}(x)$ 。

现在，为了计算代价函数的偏导数 $\frac{\partial}{\partial \theta_{i j}^{(l)}} J(\theta)$ ，我们需要采用一种反向传播算法，也就是首先计算最后一层的误差，然后再一层一层反向求出各层的误差，直到倒数第二层。

以一个例子来说明反向传播算法。

假设我们的训练集只有一个实例 $\left(x^{(1)}, y^{(1)}\right)$ ，我们的神经网络是一个四层的神经网络，其中 $K=4$ , $S_{L}=4$ , $L=4$ :

前向传播算法：

​

​

下面的公式推导过程见：

链接

我们从最后一层的误差开始计算，误差是激活单元的预测（${a^{(4)}}$）与实际值（$y^k$）之间的误差，（$k=1:k$）。
我们用$\delta$来表示误差，则：$\delta^{(4)}=a^{(4)}-y$
我们利用这个误差值来计算前一层的误差：$\delta^{(3)}=\left({\Theta^{(3)}}\right)^{T}\delta^{(4)}\ast g’\left(z^{(3)}\right)$
其中 $g’(z^{(3)})$是 $S$ 形函数的导数，$g’(z^{(3)})=a^{(3)}\ast(1-a^{(3)})$ 。而 $(θ^{(3)})^{T}\delta^{(4)}$ 则是权重导致的误差的和。下一步是继续计算第二层的误差：
$ \delta^{(2)}=(\Theta^{(2)})^{T}\delta^{(3)}\ast g’(z^{(2)})$
因为第一层是输入变量，不存在误差。我们有了所有的误差的表达式后，便可以计算代价函数的偏导数了，假设$λ=0$，即我们不做任何正则化处理时有：
$\frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)=a_{j}^{(l)} \delta_{i}^{l+1}$

重要的是清楚地知道上面式子中上下标的含义：

$l$ 代表目前所计算的是第几层。

$j$ 代表目前计算层中的激活单元的下标，也将是下一层的第$j$个输入变量的下标。

$i$ 代表下一层中误差单元的下标，是受到权重矩阵中第$i$行影响的下一层中的误差单元的下标。

如果我们考虑正则化处理，并且我们的训练集是一个特征矩阵而非向量。在上面的特殊情况中，我们需要计算每一层的误差单元来计算代价函数的偏导数。在更为一般的情况中，我们同样需要计算每一层的误差单元，但是我们需要为整个训练集计算误差单元，此时的误差单元也是一个矩阵，我们用$\Delta^{(l)}_{ij}$来表示这个误差矩阵。第 $l$ 层的第 $i$ 个激活单元受到第 $j$ 个参数影响而导致的误差。

使用神经网络时的步骤：

网络结构：第一件要做的事是选择网络结构，即决定选择多少层以及决定每层分别有多少个单元。

第一层的单元数即我们训练集的特征数量。

最后一层的单元数是我们训练集的结果的类的数量。

如果隐藏层数大于1，确保每个隐藏层的单元个数相同，通常情况下隐藏层单元的个数越多越好。

我们真正要决定的是隐藏层的层数和每个中间层的单元数。

训练神经网络：

1. 参数的随机初始化
2. 利用正向传播方法计算所有的$h_{\theta}(x)$
3. 编写计算代价函数 $J$ 的代码
4. 利用反向传播方法计算所有偏导数
5. 利用数值检验方法检验这些偏导数
6. 使用优化算法来最小化代价函数

练习

import matplotlib.pyplot as plt
import numpy as np
import scipy.io as sio
import matplotlib
import scipy.optimize as opt
from sklearn.metrics import classification_report#这个包是评价报告

def load_data(path, transpose=True):
    data = sio.loadmat(path)
    y = data.get('y')  # (5000,1)
    y = y.reshape(y.shape[0])  # make it back to column vector

    X = data.get('X')  # (5000,400)

    if transpose:
        # for this dataset, you need a transpose to get the orientation right
        X = np.array([im.reshape((20, 20)).T for im in X])

        # and I flat the image again to preserve the vector presentation
        X = np.array([im.reshape(400) for im in X])

    return X, y

X, y = load_data('ex3data1.mat')

print(X.shape)
print(y.shape)

(5000, 400)
(5000,)

def plot_an_image(image):
#     """
#     image : (400,)
#     """
    fig, ax = plt.subplots(figsize=(1, 1))
    ax.matshow(image.reshape((20, 20)), cmap=matplotlib.cm.binary)
    plt.xticks(np.array([]))  # just get rid of ticks
    plt.yticks(np.array([]))
#绘图函数

pick_one = np.random.randint(0, 5000)
plot_an_image(X[pick_one, :])
plt.show()
print('this should be {}'.format(y[pick_one]))

this should be 8

def plot_100_image(X):
    """ sample 100 image and show them
    assume the image is square

    X : (5000, 400)
    """
    size = int(np.sqrt(X.shape[1]))

    # sample 100 image, reshape, reorg it
    sample_idx = np.random.choice(np.arange(X.shape[0]), 100)  # 100*400
    sample_images = X[sample_idx, :]

    fig, ax_array = plt.subplots(nrows=10, ncols=10, sharey=True, sharex=True, figsize=(8, 8))

    for r in range(10):
        for c in range(10):
            ax_array[r, c].matshow(sample_images[10 * r + c].reshape((size, size)),
                                   cmap=matplotlib.cm.binary)
            plt.xticks(np.array([]))
            plt.yticks(np.array([]))  
            #绘图函数，画100张图片

plot_100_image(X)
plt.show()

raw_X, raw_y = load_data('ex3data1.mat')
print(raw_X.shape)
print(raw_y.shape)

(5000, 400)
(5000,)

准备数据

训练模型

进行预测

神经网络模型图示